El tamaño y la relación de los distintos rectángulos que componen la doble página nunca son arbitrarios, sino que están dictados bien por razonas prácticas, bien por el valor estético o simbólico que puedan tener en el mundo cultural en que hayan sido diseñados. Si en la actualidad el tamaño y las proporciones de esos rectángulos están determinados por las condiciones de legibilidad, los tamaños estándar del papel y el precio final del libro, en la época del libro manuscrito en pergamino aparentemente no existe otra limitación que el tamaño de la piel, el uso que pretenda darse a cada manuscrito concreto y el capricho del artesano, y por lo tanto cualesquiera combinaciones deberían ser posibles. Sin embargo, lo cierto es que de todas esas casi infinitas teóricas posibilidades de combinación, en la práctica se repiten una y otra vez las mismas proporciones, que forman un número relativamente pequeño.
Y casi todas estas proporciones repetidas una y otra vez siguen reglas matemáticas. Algunas de ellas pueden calificarse como “racionales”, pues siguen proporciones “racionales”: 1/2, 2/3, 3/4, 5/8 y 5/9 son las más corrientes. Otras son “irracionales”, en cuanto que están regidas geométricamente por números irracionales: 1/Phi (regla de oro, de la cual 5/8 es una aproximación), 1/√2, 1/√3, 1/√5, rectángulo pentagonal…
Por supuesto, también se hallan libros que aparentemente no siguen ninguna de las proporciones explicables geométricamente. Esas superficies han sido denominadas por Tschichold “arbitrarias”1.
Para comprender esta recurrencia hay que tener en cuenta que una página escrita es el resultado de una serie de exigencias formales (legibilidad fundamentalmente, pero también otras como el destino final del manuscrito como producto de exposición o lectura privada, producto de lujo y ostentación o estrictamente funcional…), pero además es fruto de un desarrollo cultural previo. Este desarrollo cultural explica por ejemplo por qué Gutenberg prefiere una página en proporción 2/3, o que durante el renacimiento rara vez se utilice la proporción 1/√2, que había sido bastante corriente durante la Edad Media.

A continuación se describen las superficies armónicas más comunes en los códices medievales y el modo de obtenerlas geométrico more.
Se obtiene partiendo de un cuadrado (ABCD), al cual se divide en dos partes iguales mediante una línea recta (EF). El punto F sirve entonces de centro de una circunferencia, cuyo radio es la diagonal FC. Luego, se prolonga la línea del lado AD y se traza un arco (CG) con el compás, hasta que corte dicha línea. Esta viene a ser la base del rectángulo. A continuación se establece el lado HG en ángulo recto con la nueva base. El cierre de la figura se consigue prolongando el lado BC hasta el punto H. Si se suprime el cuadrado original, lo que queda seguirá siendo un rectángulo áureo (DCHG).
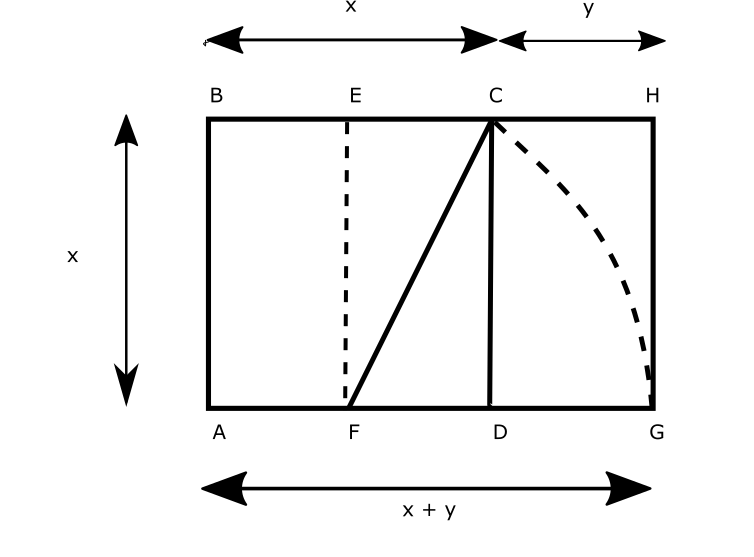
Si dividimos la longitud del lado mayor entre la del lado menor se obtiene un cociente de 1,618. Esta cifra sirve para establecer la ratio 1:1,618 (= 0,618), que se conoce como “sección áurea”. Los tres términos del rectángulo que produce constituyen una “proporción continua” (α/β = β/γ).
Es el resultado de yuxtaponer por su hipotenusa dos triángulos rectángulos de proporción 3:4:5. Produce un rectángulo de proporción 4:3 (=1,333…).
Partiendo de un cuadrado perfecto (ABCD), se toma cualquiera de sus diagonales, que se superpone a uno de sus lados, para formar el lado mayor de un rectángulo, cuyo lado menor mantiene la longitud del lado del cuadrado inicial. En este nuevo rectángulo la longitud del lado mayor es el lado menor por √2.
Este rectángulo, cuya proporción es 1/√2, tiene la peculiaridad de que si se corta por la mitad en el sentido de su lado menor o se duplica en el sentido de su lado mayor mantiene exactamente la misma proporción. De hecho, esta es la proporción del moderno sistema DIN.
La proporción invariable, desconocida o al menos ignorada en el mundo librario bizantino (como en general en la tradición tardo antigua), se va imponiendo en Occidente durante la Edad Media, al menos desde el siglo VIII2.
Si repetimos la operación con el rectángulo resultante, proyectando sobre el lado mayor la longitud de su diagonal, obtendremos un rectángulo en el que el lado mayor es el lado menor por √3, y así sucesivamente.
En realidad, las únicas fuentes que documentan algoritmos de construcción de la página se limitan a un número exiguo de recetas que además no se expresan en términos de relaciones “notables”.
En el occidente latino las recetas conservadas son dos: las denominadas “receta de Saint-Remi” (Paris, BNF, Ms. lat. 11884)3, del s. IX, y la “Receta de Munich” (Bayerische Staatsbibliothek, Clm 7755)4, del XV (a las que podrían añadirse otras dos en italiano, del siglo XV5, si bien una de ellas parece responder a una tardía especulación matemática6)7. Las dos recetas, estructuralmente muy diferentes entre sí, se refieren a páginas de fisonomía un tanto diversa: ancha en el ejemplo más antiguo y alargada y tendente a la proporción invariable en el más moderno. Ambos textos se expresan en términos de relación y no de valores absolutos, por lo que son aplicables a códices de cualquier dimensión.
La “Receta de Saint-Remi” especifica lo siguiente:
Taliter debet fieri quaternionis forma, quinta parte longitudinis, quarta latitudinis. Quintam partem da inferiori vel anteriori margini, et ipsam quintam partem divide in III et dabis II superiori, subtracta I. Rursus ipsas II partes divide in tres, dabisque duas posteriori margini, subtrahendo unam. Huic comprar erit si media interfuerit. Lineas vero iuxta rationem scripturae divides, quia maior scriptura latioribus, minos autem strictioribus lineis indiget.
Prescribe observar las siguientes proporciones:
La aplicación de estos criterios operativos origina las siguientes áreas armónicas:
Aunque no se han encontrado manuscritos que respondan con exactitud a este modelo teórico, el testimonio resulta interesante porque nos confirma una vez más la existencia de normas destinadas a crear superficies proporcionales sin necesidad de que el artesano tuviera unos conocimientos matemáticos precisos.
La receta de Munich observa lo siguiente:
Ad faciendum spacia in libris. Nota quod spacia superiora et circa ligaturam sunt equalia. Spacium inferius sit in duplo lacius sicut unum de prioribus. Item spacium extremum habeat tres partes sic, quod sit minus quam inferius in una quarta.
Lo cual se limita a prescribir (siempre en términos de relaciones y no de valores absolutos) las dimensiones relativas de los márgenes, dando al artesano libertad para fijar a su gusto la relación entre la altura y la anchura de la página, aunque solo aparentemente, si se tiene en cuenta la abrumadora tendencia de los manuscritos bajomedievales a usar el rectángulo de proporción creciente 1/√2.
Este canon constructivo, elegante y depurado, utilizado para libros lujosos, origina una distribución del espacio muy equilibrada, pues la armonía entre las superficies de la caja del pautado y de la página se establece gracias a la igualdad de sus proporciones, pues, si se parte de una superficie de proporción 2:3, la altura de la caja de escritura coincide con la anchura de la página y los márgenes se ajustan a la relación 2:3:4:6. Si la superficie de partida tiene otras proporciones, el resultado será también un reparto armonioso de negro sobre blanco, pero se pierde la mencionada igualdad de proporciones.
Empíricamente se tenía noticia de su existencia, pero se desconocía el principio matemático y el diseño geométrico en que se basaba el procedimiento para construirlo, hasta que en 1953 fue descubierto por Jan Tschichold.
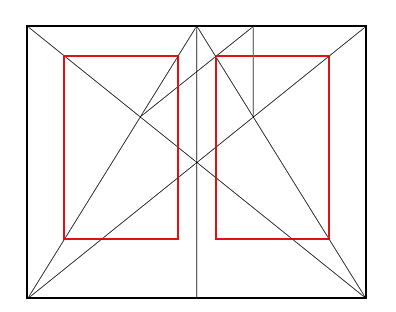
Partiendo de la doble página, se trazan las diagonales correspondientes a cada una de las páginas y a la doble página. Después, partiendo del punto de intersección de la diagonal de la página y la diagonal de la doble página se traza una línea vertical hasta el borde superior, y desde el punto en que la línea vertical corta el borde de la hoja otra línea recta hasta el punto de intersección de las diagonales en la página opuesta. El punto de intersección de esta última línea con la diagonal de la página servirá entonces como punto de partida para trazas las líneas de la caja de justificación: la de cabecera correrá en horizontal, paralela al borde superior de la hoja, desde el punto indicado hasta su intersección con la diagonal de la doble página; a partir de ese punto, la línea de justificación exterior baja en vertical, hasta interceptar la diagonal de la página, donde comienza la línea de justificación inferior, que corre de nuevo en horizontal, en paralelo a la línea de cabeza, y finalmente la línea interior corre en vertical desde el punto inicial hasta interceptar con la línea de pie.
Como puede apreciarse, el compás, junto con la regla, es el instrumento indispensable de la mise-en-page. En la ilustración que acompaña estas líneas, que procede de un homiliario del siglo XII (Berlin, Staatsbibliothek Preussischer Kulturbesitz, MS Theol. Lat. Fol. 270, fol. 224v) vemos un monje sosteniendo un compás de tres puntas que probablemente se usaba para reproducir las proporciones fijadas entre la primera y la segunda punta y entre la segunda y la tercera.

También se conoce un compás de cuatro puntas o compás de proporciones, cuyas puntas se utilizaban por parejas para trasladas las proporciones deseadas.
Igual que en el terreno paleográfico cada lengua o asunto manifiesta unas determinadas preferencias en la elección de los tipos de letra, la elección del diseño de página parece seguir unas pautas similares. Por ejemplo, Carla Bozzolo, Dominique Coq, Denis Muzerelle y Ezio Ornato8 han encontrado patrones de uso diferentes en los manuscritos franceses de finales de la Edad Media, dependiendo de que hayan sido escritos en latín o en francés, por lo que distinguen entre una “page savante” y una “page vulgaire”: en tanto que en los manuscritos latinos la relación entre anchura y altura es de 1/√2 (esto es, entorno a 0,707), que es precisamente una de las proporciones geométricas identificadas por Tschihold, los manuscritos franceses tienden a tener una página algo más larga (1/1,423, o sea, 0,7022 de media). Y la diferencia es aún más evidente si se considera la proporción de la caja de escritura: 0,682 de media para los manuscritos latinos frente a 0,727 para los franceses. Además, en los manuscritos franceses la caja de escritura no se ensancha cuando la disposición de texto tiene lugar a doble columna (0,691 para los manuscritos latinos, 0,726 para los franceses, donde además el espacio entre ambas columnas es algo más ancho, lo cual indica que aquí el copista no estaba interesado en compensar el espacio de escritura que se pierde en el intercolumnio haciendo los márgenes algo más estrechos). Y es que en el caso de los manuscritos en lengua vernácula los artesanos pueden expresarse más libremente y pueden utilizar en sus diseños medidas más próximas a las dimensiones naturales de las pieles o las formas comúnmente utilizadas para la fabricación del papel.
En definitiva, considerando en conjunto los aspectos geométricos de la mise-en-page, la página se define como un conjunto equilibrado de rectángulos (al menos en un libro bien diseñado). Y ese equilibrio está determinado por la extensión respectiva de los rectángulos y la armonía entre sus proporciones.
Este equilibrio y armonía se perciben instintivamente, y la razón parece ser fisiológica: la estimación que realiza el ojo de las longitudes relativas de los lados adyacentes de un rectángulo (A-B, A-D) es en última instancia reducible a la medida instintiva de la duración relativa de dos intervalos de tiempo. Lo que se aprecia a nivel subconsciente es la ratio del tiempo que requiere la línea de visión para pasar de A a B y de A a D, y estos intervalos son instintivamente medidos por los relojes corporales internos. Mientras que el foco de visión pasa de A a B, un cierto número de impulsos nerviosos pasa a través de los nervios ópticos en un período de tiempo proporcional al esfuerzo muscular del globo ocular. La experiencia armoniosa que se percibe cuando concurren ciertas longitudes obedece, pues, en última instancia a la misma razón por la cual ciertos intervalos musicales son percibidos como más armoniosos, cuando son reducibles a la proporción de números enteros pequeños, y son exactamente la octava (ratio de la frecuencia 2/1), tercera mayor (5/4) y sexta mayor (8/5)9.
1. Jan Tschichold, “Non-arbitrary proportions of page and type area”, A.S. Osley (ed.), Calligraphy and Paleography. Essays presented to Alfred Fairbank, London, Faber and Faber, 1965, pp. 179-191; “Correlation between book page and type area”, Jan Tschihold, The form of the book. Essays on the morality of good design, Vancouver, Hartley & Marks, 1991, pp. 36-63.↩
2. J.P. Gumbert, “The Sices of Manuscripts. Some Statistics and Notes”, A.R.A. Croiset van Uchelen (ed.), Helinga Festschrift /Feestbundel / Mëlanges. Forty-three Studies in Bibliography Presented to Prof. Dr. Wytze Hellinga on the Occasion of his Retirement from the Chair of Neophilology in the University of Amsterdam at the end of tye year 1978, pp. 277-288.↩
3. D. Muzerelle, “Normes et recettes de mise en page dans le codex pré-carolingien”, en A. Blanchard (ed.), Les débuts du codex. Actes de la journée d’études organisée à Paris les 3 et 4 juillet 1985, Turnhout, 1989, pp. 125-156.↩
4. B. Bischoff, “Zur Screib- und Buchtechnik des Spätmittelalters, II. Regel für die Seiteneinteilung (Fünfzehntes Jahrhunderts)”, en Anécdota novissima. Texte des vierten bis sechzehnten Jahrhunderts, Stuttgart, 1984, pp. 237-240.↩
5. P. Cherubini, “Una nuova ricetta in volgare per rigare la pagina (secolo XV)”, Miscellanea Bibliothecae Apostolicae Vaticanae 11, Città del Vaticano, 2004 (Studi e Testi 423), pp. 241-258.↩
6. Giorgio Montecchi, “Le dimensioni del libro secondo la Theorica et practica di Sigismondo Fanti”, en Il libro nel Rinascimento. Saggi di bibliologia, Milano, 1997, Roma, 19972, pp. 93-107↩
7. Marilena Maniaci, “Ricette di costruzione della pagina nei manoscritti greci e latini”, Scriptorium 49 (1995), pp. 16-41; id. “Ricette e canoni di impaginazione del libro medievale. Nuove osservazione e verifiche”, Scrineum Rivista 10 (2013), pp. 1-48.↩
8. Carla Bozzono, Dominique Coq, Denis Muzerelle & Ezio Ornato, “Page savante, page vulgaire: Étude comparative de la mise en page des livres en latin et en français écrits ou imprimés en France au XVe siècle", La face cachée du livre médiéval. L’histoire du livre vue par Ezio Ornato, ses amis et ses collègues, Roma, Viella, 1997, pp. 509-517.↩
9. H.E. Huntley, The Divine Proportion. A Study of Mathematical Beauty, New York, Dover Publications, 1970, pp. 52-56.↩