5. Composición de la página

5.6. La "Geometría teológica" en los códices medievales

Número y proporción en la teología medieval

En el mundo antiguo y medieval la geometría es a menudo utilizada como una metáfora del orden universal y los números poseen un significado místico añadido a su función de indicar la cantidad. Por ejemplo, el uno no es propiamente un número, sino el principio de los números¹, y contiene en sí todas las cosas, y por eso es el símbolo numérico de Dios Creador. El propio deis Creador es descrito en la Biblia como un geómetra:

Cuando colocaba los cielos, allí estaba yo (i.e., la Sabiduría), cuando trazaba la bóveda sobre la superficie del océano (Prov 8:27).

Pero tú regulaste todo con medida, número y peso (Sab 11:20).

Por eso para los Padres de la Iglesia los números pueden constituir un instrumento con el que el intelecto puede transcender de lo terrestre a lo celeste². En los números san Agustín veía una imagen de lo absoluto, y es a través de las formas visibles como lo invisible se manifiesta a los hombres³, y en consecuencia utilizó el círculo (tras descartar el triángulo y el cuadrado) como la forma geométrica más adecuada para representar la unidad del alma, por ser una superficie limitada exclusivamente por la única línea indivisible⁴. Y Casiodoro, en un pasaje que debió de calar hondo en la conciencia de su tiempo, pues fue reutilizado en el siglo IX por Rabano Mauro⁵, especifica que:

Nunc ad geometricam veniamus, quae est descriptio contemplativa formarum, documentum etiam visibile philosophorum; quod ut preconiis efferant, Jovem suum in operibus propriis geometrizare testantur. Quod nescio utrum laudibus an vituperationibus applicetur, quando quod illi pingunt in pulvere colorato, Jovem facere mentiuntur in caelo. Quod si vero Creatori et omnipotenti Domino salubriter applicetur, potest haec sententia forsitan convenire veritati geometrizat enim, si fas est dicere, sancta Trinitas, quando creaturis suis, quas hodieque fecit existere, diversas species formulasque concedit; quando cursus stellarum potentia veneranda distribuit, et statutis lineis facit currere quae moventur certaque sede quae sunt fixa constituit; quidquid enim bene disponitur atque completur, potest disciplinae huius qualitatibus applicari⁶.
Pasemos ahora a la geometría, que es la descripción contemplativa de las formas, y también el modelo visual de los filósofos, porque atestiguan, según relatan en los más célebres panegíricos, que su Júpiter en sus propias obras se servía de la geometría. E ignoro si esto ha de aplicarse para alabanza o para vituperación, cuando mencionan que Júpiter hace en el cielo lo que ellos representan en arena coloreada. Porque si verdaderamente ha de aplicarse salvíficamente a Dios creador y omnipotente, acaso francamente puede convenir a la verdad. Pues hace geometría la divinidad –si se me permite expresarlo así– cuando concede figuras y composiciones a su criatura, a la cual incluso hasta hoy mantiene en la existencia; cuando con poder digno de admiración distribuyó los cursos de las estrellas e hizo pasar en líneas preestablecidas a las estrellas que se mueven, y designó en un lugar determinado a las que están fijas.

Y en algún momento entre el siglo VI y VII Apponio en su comentario sobre el Cantar de los Cantares afirma que disciplina autem geometricae et arithmeticae artis mensura et numero omnem creaturam docet constare⁷.

Por eso las formas geométricas se utilizaban para construir analogías de la Divinidad. En definitiva, los números y su significado eran una de las claves para transcender con el intelecto el mundo de los sentidos, y así tratar cuestiones ontológicas recurriendo a la geometría. Especialmente las imágenes geométricas se usaban para discutir cuestiones concernientes al estatus ontológico de nociones generales (universales) en comparación con los objetos materiales. Así aparece al menos en autores tan relevantes como Macrobio, Boecio y Juan Escoto Eriúgena⁸.

Del mismo modo, la geometría es una herramienta para la meditación sobre la unidad metafísica (que para la religión cristiana no puede ser otra cosa sino Dios), un modo de simbolizar visualmente y contemplar la esencia incomprensible⁹. La esencia de la unidad inaprehensible suele ser representada por el círculo (recuérdese que tanto la longitud de la circunferencia como el área del círculo están determinados por el número irracional Pi), aunque su manifestación es el cuadrado: este, formado por dos pares perfectamente iguales aunque opuestos de ángulos, es perfectamente simétrico, comprensible (puede medirse exactamente), y representa las cuatro orientaciones primarias, los cuatro elementos (por eso se lo utiliza como expresión geométrica de la Naturaleza).

En las formas geométricas concurre además el simbolismo de los números incrementado por el hecho de que en ellas estos interactúan estableciendo relaciones que se expresan en ratios y proporciones. La ratio es la comparación entre dos números, longitudes o magnitudes diferentes, a/b); la proporción es la relación de equivalencia entre dos ratios (a/b:c/d), y por ello representa un nivel más sutil y profundo de inteligencia que la simple percepción de la diferencia (ratio)¹⁰.

Propuesta de interpretación de algunas superficies armónicas frecuentes en la mise-en-page de los manuscritos medievales

El empleo tanto de la aritmología como de las proporciones armónicas de las figuras geométricas es bien conocido en el diseño de catedrales y otros edificios, que utilizan sus connotaciones de perfección formal y misticismo numérico y las trasladan a los espacios que construyen¹¹. Por ejemplo, la capilla del palacio de Carlomagno en Aquisgrán está diseñada sobre las formas de un cuadrado y un círculo, y su sección longitudinal está estructurada sobre dos círculos de 48 pies inscritos en un círculo mayor de 96 pies.

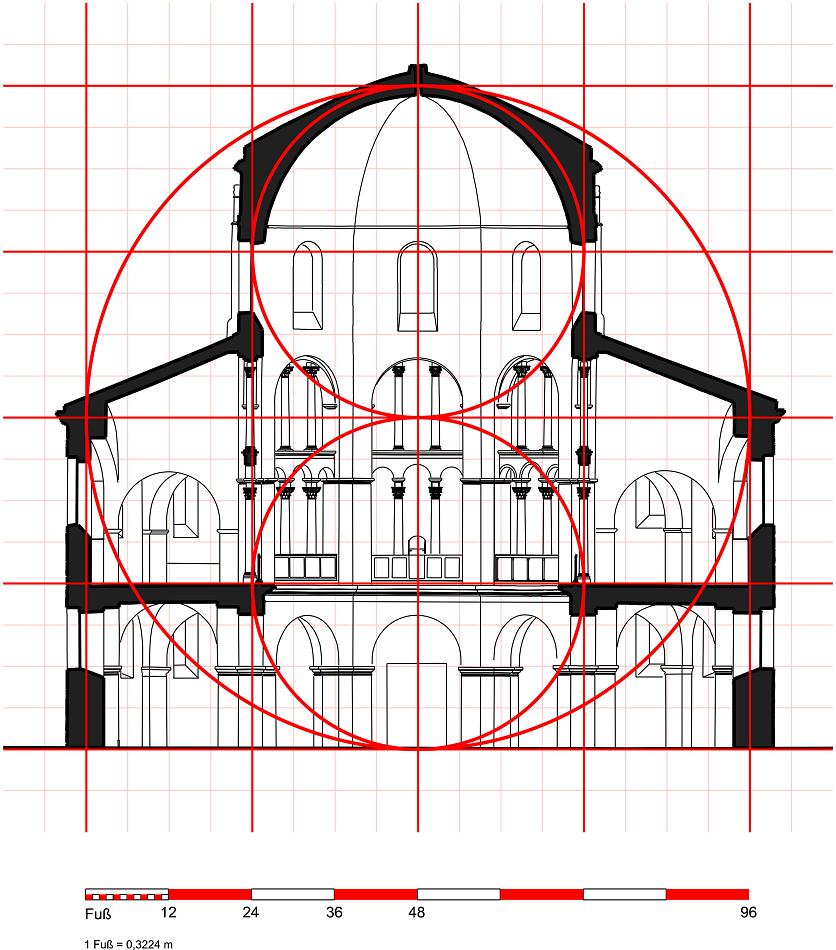
Sin embargo, en codicología el estudio de las mismas superficies y proporciones, aunque conocido, no a rendido los mismos resultados.

Si los números eran entendidos como signos de realidades espirituales y las figuras geométricas jugaban un papel fundamental en el simbolismo de las edificaciones religiosas, igual que en los constructores de catedrales, existió sin duda entre los mejores maestros de escriptorio una intencionalidad de transcender la mera estética y proporcionar a los lectores de sus libros una herramienta de meditación a través de las simple contemplación de las formas geométricas.

Ya se ha comentado más arriba que según la definición de Boecio (tomada de Nicómaco de Gerasa), proporción es la relación de equivalencia entre dos ratios, y que ratio es a su vez la comparación entre dos números. Es decir, que en principio dos ratios implican cuatro números diferentes (a/b::c/d, ej.: 2/4::3/6), relacionados a un nivel que en el pensamiento griego se define como analogía¹², y recuérdese que cuatro es precisamente el número simbólico para expresar la naturaleza finita, racional y mensurable del mundo creado: en él se hallan las claves de toda la naturaleza¹³. En la matemática pitagórica, una proporción de este tipo recibe el calificativo de “proporción discontinua”.

Ahora bien, la contemplación de una proporción puede ayudar a la mente a trascender el mundo creado, cuando en la proporción los elementos implicados han sido reducidos de cuatro a tres, por medio de establecer la identidad del segundo término con el tercero: a/b::b/c (o a:b:c). Los griegos denominaron a este tipo de proporción de tres términos “proporción continua” y recuérdese que en la matemática pitagórica el tres es el número en acción, el primer número primo después de la mónada y de la díada, y se asocia a todo lo que implica “composición” en la naturaleza, y por ende al conocimiento¹⁴. Pero en el mundo cristiano el tres evocaba sin duda la Trinidad.

Entre las superficies armónicas identificadas por Gilissen y Tschichold una de las más asiduamente utilizadas en los manuscritos medievales es la llamada proporción áurea, que se define por el número irracional Phi (1,618…). Phi puede definirse aritméticamente como el número cuyo cuadrado se obtiene sumando 1 al número inicial (Phi² = Phi + 1), de donde Phi = (√5+1)/2¹⁵. Pero Phi tiene también una definición geométrica que para nuestro propósito es todavía más interesante. Phi o proporción áurea tiene la peculiaridad de que es la única proporción que puede definirse con solo dos términos: a/b::b/(a+b), es decir, que la ratio entre a y b es idéntica a la ratio entre b y la suma de a + b. Tres que proceden de dos y que se subsumen en uno… Geométricamente no se puede estar más cerca del misterio teológico de la Santísima Trinidad, y misterio también geométrico, porque Phi es un número irracional, que no se puede medir, aunque se pueda representar, y que es expresión de la proporción sobre la que se funda la experiencia del conocimiento o logos, y Logos (=Lat. Verbum) es también la expresión de Dios-Hijo: In principio erat Verbum, et Verbum erat apud Deum, et Deus erat Verbum (Io 1:1).

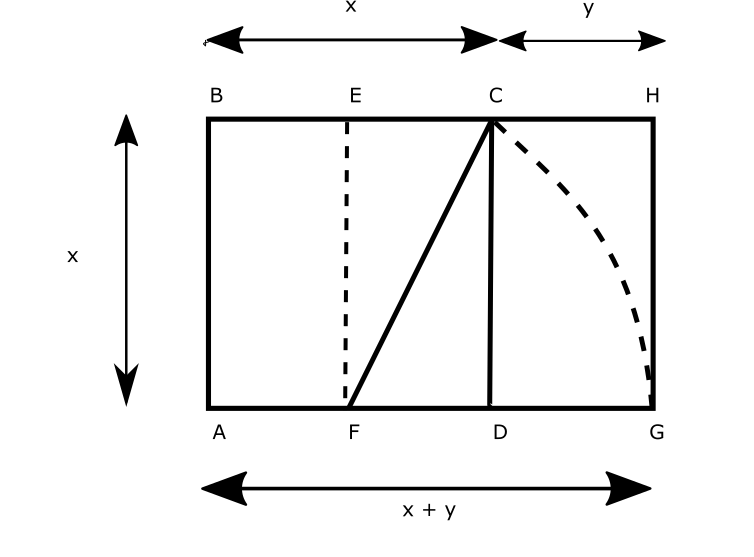
La historia del arte religioso proporciona abundantes ejemplos del empleo de Phi como medio para alcanzar balance en el diseño compositivo. Según Frederik Macody Lund, numerosas estructuras arquitectónicas góticas están diseñadas siguiendo la dorada proporción, entre otras las catedrales de Chartres, Laon y Notre-Dame de París, pero también las esbeltas proporciones de las estatuas de estas mismas catedrales se corresponden con ella¹⁶.

En el terreno codicológico Robert Stevick ha examinado algunas páginas iluminadas de manuscritos, con el propósito de descubrir las técnicas de diseño de sus autores. Su conclusión es que la dorada proporción es la piedra angular del diseño, y que la impaginación está planificada utilizando instrumentos similares, aunque de menor tamaño, a los usados por los constructores de catedrales¹⁷.

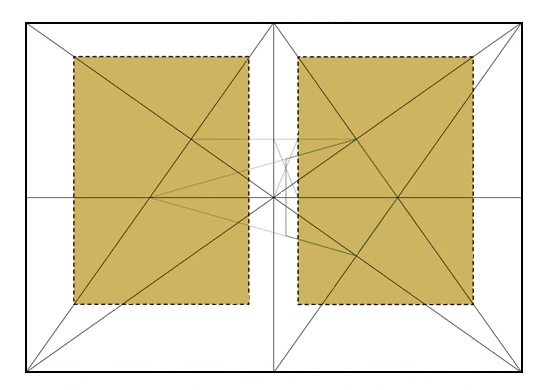
Otra de las superficies armónicas identificadas en los códices es el rectángulo de proporción creciente. Se define por tener su lado mayor la longitud de la diagonal de un cuadrado formado a partir de su lado menor (proporción 1:√2).

La matemática de esta figura también se remonta a Grecia, donde se conoció el fenómeno como “expansión gnómica”. Según Herón de Alejandría, un gnomon es una figura que añadida a la figura original produce una figura similar a la figura original, y la contemplación de esta figura conduce a la comprensión de una de las formas más conocidas de crecimiento natural: el crecimiento por acreción o incremento acumulativo, en el cual la antigua forma está contenida dentro de la nueva¹⁸. Nos encontramos aquí frente a un proceso de expansión indefinida en el que cada uno de los términos contiene, superados, a cada uno de los que le han precedido y preludia a su vez el paso siguiente. No en vano este es el principio que sigue el actual formato DIN, en el cual cada tamaño produce exactamente el tamaño siguiente al ser doblado por la mitad de su lado mayor. Pero además el empleo de √2 le confiere un significado especial, al menos a juzgar por la práctica equivalente en la arquitectura religiosa, donde los maestros constructores vieron una especie de término medio entre 1 y 2, considerados como dos extremos opuestos (lo cual es precisamente la definición aristotélica de la virtud). 1:√2:2 es exactamente la proporción geométrica según es descrita por Boecio, y en los claustros define la relación entre el cuadro interior y el exterior, de modo que caminar por él podría ser interpretado como recorrer el camino de la virtud que conduce al Reino de los Cielos. En un códice, semejante proporción estaría representada por tres rectángulos de proporción creciente 1:√2, cuyo diseño se corresponde con el denominado “canon secreto”, según se muestra en la siguiente figura, donde, además, la proporción de las anchuras de los márgenes es 2:3:4:6, que constituyen la proporción armónica según fue definida por Boecio.

---

^{1. “Número es la multitud constituida por unidades”, “el uno u no el número es el origen de los números”; “la unidad no es número, pero a partir de ella se siguen los números”, Rabano Mauro, De computo 3.↩}

^{2. San Agustín, De ordine 15, 42-43 (Geometria et Astronomia); De civitate Dei 11, 30.↩}

^{3. San Agustín, De Trinitate 2,5,10.↩}

^{4. San Agustín, De quantitate anima 10-16.↩}

^{5. De institutione clericorum III, 23.↩}

^{6. Cassiodori Senatoris Institutionis, ed. Roger A.B. Mynors, Oxford, Clarendon Press, 1937, 2.5.11, p. 150.↩}

^{7. Apponius, In Canticum Cantocorum expositio, CCCM 19, Turnhout, Brepols, 1986, p. 217. Cit. Eugeny A. Zaitsev, “The meaning of early medieval Geometry: from Euclid and Surveyors’ manuals to Christian Philosophy”, Isis 90/3 (1999), pp. 522-533, cit. p. 538.↩}

^{8. Zaitsev, “The meaning of early medieval Geometry”, pp. 544-545.↩}

^{9. Robert Lawlor, Sacred Geometry. Philosophy, London, Thames & Hudson, 1982 (reimpr. 2002), pp. 16 y 22.↩}

^{10. Lawlor, ibid., p. 44.↩}

^{11. Mari-Pierre Terrien, “Religious architecture and Mathematics during the Late Antiquity”, T. Koetsier & L. Bergmans (eds.), Mathematics and the Divine: a Historical Study, Amsterdam, Elsevier, 205, pp. 147-160.↩}

^{12. Lawlor, op. cit., p. 44.↩}

^{13. J.F. Mattéi, “Nicomacus of Gerasa and the Arithmetic Scale of the Divine”, T. Koetsier ∓ L. Bergmans (eds.), Mathematics and the Divine: a Historical Study, Amsterdam, Elsevier, 2005, pp. 123-132, cit. p. 128.↩}

^{14. Mattéi, op. cit., p. 128.↩}

^{15. O (√5-1)/2.↩}

^{16. James Snyder, Medieval Art: Painting, Sculpture, Architecture, 4th-14th Century, Upper Saddle River, N.J. Prentice Hall, 1989, p. 260.↩}

^{17. Robert D. Stevick, “The Echternach Gospels’ Evangelist Symbol Pages: Forms from ‘The Two True Measures of Geometry’”, Peritia 5 (1986), pp. 284-308.↩}

^{18. Lawlor, op. cit., p. 65.↩}